TI-Nspire & Lua / 古典的ルンゲクッタ法 4 / クロージャを使って初期値を更新しながら 1 ステップずつの計算を繰り返すが、1 ステップをさらに内部分割する

function rk(func, t0, x0, step, numOfDiv) -- numOfDiv は 1 ステップの内部分割数 
   local numOfDiv = numOfDiv or 1
   local step     = step / numOfDiv
   local stepDiv2 = step / 2
   local stepDiv6 = step / 6
   local f1, f2, f3, f4

   local t0, x0    = t0, x0
   local halfPoint = t0 + stepDiv2
   local nextPoint = t0 + step
   return function()
             for i = 1, numOfDiv do
                f1 = func(t0        , x0                )
                f2 = func(halfPoint , x0 + stepDiv2 * f1)
                f3 = func(halfPoint , x0 + stepDiv2 * f2)
                f4 = func(nextPoint , x0 + step     * f3)

                t0        = nextPoint
                halfPoint = t0 + stepDiv2
                nextPoint = t0 + step
                x0        = x0 + stepDiv6 * (f1 + 2 * (f2 + f3) + f4)                
             end
             return t0, x0
          end
end

--- 確かめる。
do
local function sute(t, x)
   return x^2 - t^2 - 2 * t + 2
end

local init, from, to, step = 0, 0, 3, 1/8

local rkA = rk(sute, from, init, step, 1  ) -- 内部分割数を変えて比べてみる。t = 3 のときの真値は 3.75 である。
local rkB = rk(sute, from, init, step, 2^2)
local rkC = rk(sute, from, init, step, 2^6)

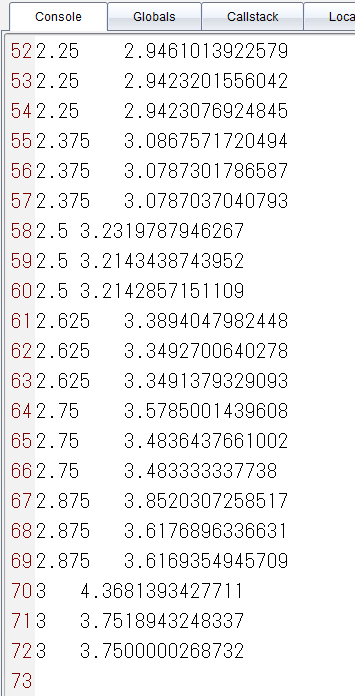
for i = 1, to/step do
   print(rkA())
   print(rkB())
   print(rkC())
end
end